Wyobraź sobie, że opracowałeś nowy, super efektywny algorytm. Działa o wiele lepiej niż wszystkie znane rozwiązania. Oprogramowanie, które stworzyłeś świetnie się sprzedaje, klienci są zachwyceni, a Ty wyjeżdżasz na Bahamy.

Niestety! Po miesiącu sprzedaż drastycznie spada. Kilka innych firm oferuje dokładnie to samo rozwiązanie. Ewidentnie jeden z klientów skopiował algorytm, który mu udostępniłeś. Co gorsza mają o wiele lepszą reklamę. Koniec wakacji - musisz wracać do domu wymyślać nowy produkt. Czy dało się temu zapobiec? Jedno z rozwiązań oferuje nowoczesna kryptologia badająca metody szyfrowania programów. Zaszyfrowany program ma działać dokładnie tak jak zwykły, to znaczy dla tych samych danych wejściowych ma zwracać te same wyniki. Jednak jego kod powinien być niezrozumiały dla użytkownika. Co więcej chcielibyśmy mieć matematyczny dowód na to, że rozszyfrowanie kodu programu jest tak skomplikowane jak pewien znany trudny problem obliczeniowy. Dziedzinę kryptologii zajmującą się szyfrowaniem programów nazywamy obfuskacją.

Jak opisać program?

Każdy program komputerowy możemy przedstawić jako układ logiczny, składających się z bramek cyfrowych. Układy logiczne można opisywać w sposób matematyczny przez funkcje boolowskie, czyli funkcje postaci $f: \{0,1\}^n \rightarrow \{0,1\}^m$ dla pewnych ustalonych liczb całkowitych $n$ i $m$. Rozważmy układ z rysunku

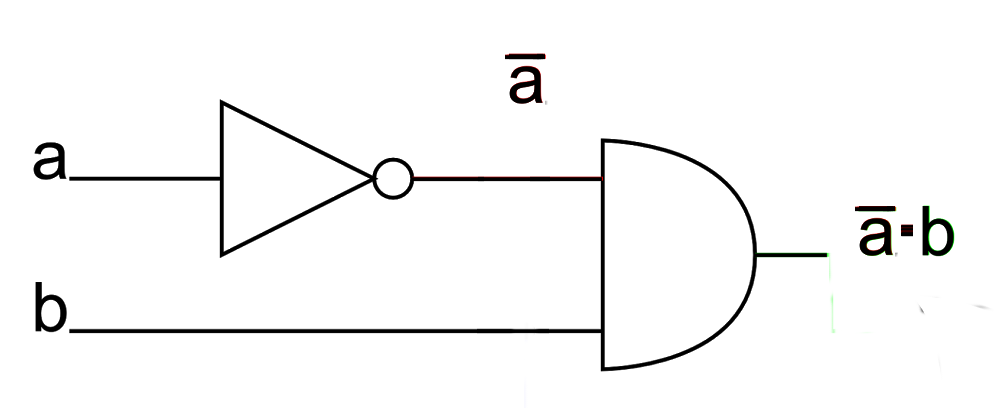
będący złożeniem dwóch bramek logicznych: NOT i AND. Bramce NOT odpowiada funkcja $f_1(a)=1-a$, a bramce AND funkcja $f_2(a,b)=a\cdot b$. Cały układ opisuje funkcja $f$ postaci:

\[f:\{0,1\}^2 \rightarrow \{0,1\} \\ f(a,b) = f_2(f_1 (a),b) = (1-a) \cdot b.\]

Zmiana postaci programu

Twierdzenie Barringtona zapewnia, że każdy układ logiczny można przedstawić jako iloczyn macierzy. Na przykład funkcja $f(a,b) = a \cdot b$ może być reprezentowana jako iloczyn macierzy w następujący sposób:

\[\begin{bmatrix} 1 & a \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 \\ 0 & b \end{bmatrix} = \begin{bmatrix} 1 & a \cdot b \end{bmatrix}.\]

Wynik działania funkcji przechowywany jest na drugiej współrzędnej wektora iloczynu. Zauważmy, że w naszej reprezentacji jednej zmiennej odpowiada jedna macierz. Chcemy aby użytkownik mógł wykonać funkcję na dowolnych danych wejściowych, zatem musimy dać mu macierze odpowiadające dowolnym wartościom zmiennych $a$ i $b$. Dlatego publikujemy pary macierzy:

\[\left( M_{a=0}=\begin{bmatrix} 1 & 0 \end{bmatrix}, M_{a=1}=\begin{bmatrix} 1 & 1 \end{bmatrix}\right), \left( M_{b=0}=\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, M_{b=1}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right).\]

Kiedy użytkownik chce wykonać program na zmiennych $a=1$ i $b=0$ wybiera macierze $M_{a=1}$ i $M_{b=0}$ i oblicza ich iloczyn

\[\begin{bmatrix} 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \end{bmatrix},\]

otrzymując poprawny wynik. Z funkcją $f_1(a)=1-a$ jest jeszcze łatwiej, ponieważ zależy tylko od jednej zmiennej wejściowej. Obliczenie będzie wyglądało następująco:

\[\begin{bmatrix} 1 & a \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 0 & -1 \end{bmatrix} = \begin{bmatrix} 1 & (1-a) \end{bmatrix}.\]

W tym wypadku druga macierz jest stała (nie zależy od żadnej zmiennej). Reprezentacja funkcji $f$ jest połączeniem reprezentacji $f_1$ i $f_2$:

\[\begin{bmatrix} 1 & a \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 \\ 1 & -1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 \\ 0 & b \end{bmatrix} = \begin{bmatrix} 1 & (1-a) \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 \\ 0 & b \end{bmatrix} = \begin{bmatrix} 1 & (1-a) \cdot b \end{bmatrix}.\]

Aby użytkownik mógł wykonać funkcję $f$ na dowolnych danych wejściowych udostępniamy mu pary macierzy:

\[\left( M_{a=0}=\begin{bmatrix} 1 & 1 \end{bmatrix}, M_{a=1}=\begin{bmatrix} 1 & 0 \end{bmatrix}\right), \left( M_{b=0}=\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}, M_{b=1}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \right).\]

Zauważmy, że w macierzach odpowiadających zmiennej $a$ jest zakodowane zaprzeczenie.

Zaszyfrowanie programu

Program macierzowy poprawnie oblicza zadaną funkcję, ale żeby był nieczytelny trzeba zaszyfrować tworzące go macierze. W wyniku szyfrowania chcemy otrzymać macierze, których elementy nie zdradzają jakie obliczenie jest wykonywane

\[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \stackrel{encrypt}{\rightarrow} \begin{bmatrix} !@\star!\circ & \star@@\#! \\ \circ!!@\star & @\dot!\star!@! \end{bmatrix}.\]

Do tego celu musimy użyć specjalnego szyfrowania, które zapewni nam dwie kluczowe własności. Po pierwsze licząc iloczyn zaszyfrowanych macierzy, chcemy otrzymać szyfrogram iloczynu

\[encrypt(M_a) \cdot encrypt(M_b) = encrypt(M_a \cdot M_b).\]

Dzięki tej własności wymnażając zaszyfrowane macierze dostaniemy poprawne wyniki. Szyfry zachowujące mnożenie nazywamy homomorficznymi ze względu na mnożenie. Po drugie chcemy mieć pewność, że wynik programu będzie możliwy do odszyfrowania, ale poszczególne macierze nie. Taką funkcjonalność otrzymamy przyporządkowując szyfrogramom stopnie. Z każdym wykonywanym mnożeniem zwiększa się stopień szyfrogramu. Dopiero po wymnożeniu wszystkich macierzy - i osiągnięciu maksymalnego stopnia - wynikowa macierz może zostać odszyfrowana. Szyfry przyporządkowujące szyfrogramom stopnie nazywamy szyframi z gradacją.

Istnieje kilka szyfrów homomorficznych z gradacją na przykład CLT13, GGH13 i GGH15. Niestety działają bardzo wolno, a zaszyfrowane macierze mają bardzo duże rozmiary. Kryptologowie z niecierpliwością czekają na nowe konstrukcje tego typu szyfrów. Może Ty taki wymyślisz?